SDGs取組事例集一覧
取組事例テーマ
錯視が解き明かす視覚の認知空間 < STEAM教育のアートと数学にフォーカスして >
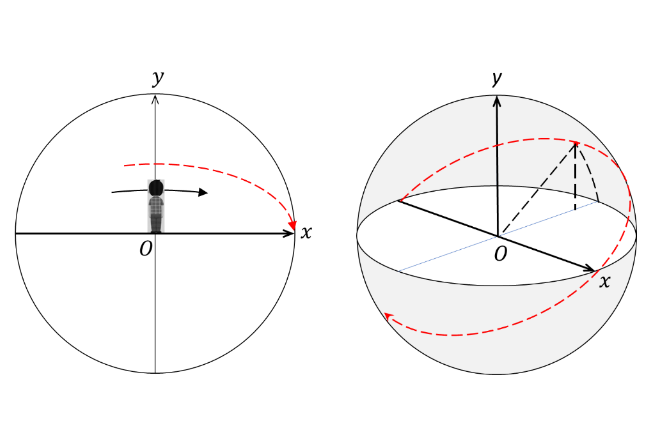
図1.平行線が交差して見える理由
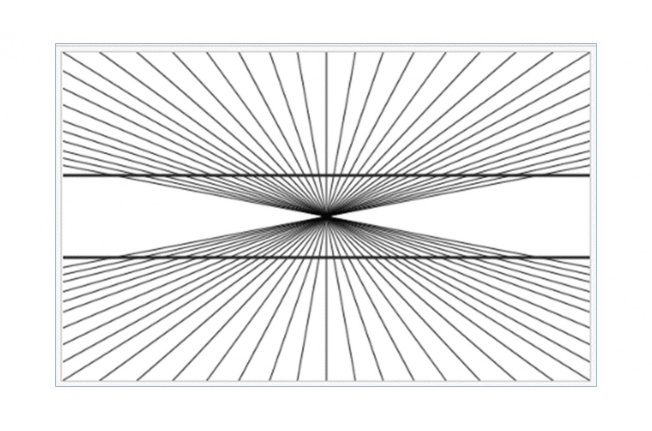
図2.ヘリング錯視 ※2
取組概要
視覚が認識している映像は実体とは少し異なる。視空間における映像は単なる幻想にすぎない。しかしながらそこには確かな物理法則が存在する。図1左のように足元から左右に伸びる直線と、これに平行な目の前の直線は無限遠で交わる。この事は目の前に見えている直線が、実は湾曲して見えていることを示唆している。図1右のように視空間がプラネタリウムのような球体で、視点が球体の中心にあれば、球面に投影された垂直な直線も立体的には湾曲している。従って平行線が交わる現象も、球面上では当たり前の現象となる。この事から視空間の形状は球体であり、物理空間とは全く異なる形状と言える。物理空間では平行線は決して交わらない。しかしながら視空間を忠実に再現した写真の中では平行線は交わる。言い換えると、平行線の延長線上に消失点という交点が存在する。このため直方体を立体的に描く時、つまり視空間が丸いことを意識して直方体を描くと、消失点から延びる補助線に合わせて直方体の各辺は傾く。これが透視図法(遠近法)である。我々は日々、遠近法という幻想から、視空間が丸いことを学んでいる(※1)。この事実をヘリング錯視(図2、※2)は教えてくれる。
今後の展開
視空間の数式化
担当者
-
特任准教授西本 博之高知大学 医学部附属病院次世代医療創造センター ヘルスケアイノベーションコース担当
ホームページ























